Bound state

In physics, a bound state describes a system where a particle is subject to a potential such that the particle has a tendency to remain localised in one or more regions of space. The potential may be either an external potential, or may be the result of the presence of another particle.

In quantum mechanics (where the number of particles is conserved), a bound state is a state in Hilbert space that corresponds to two or more particles whose interaction energy is less than the total energy of each separate particle, and therefore these particles cannot be separated unless energy is spent. The energy spectrum of a bound state is discrete, unlike the continuous spectrum of isolated particles. (Actually, it is possible to have unstable bound states with a positive interaction energy provided that there is an "energy barrier" that has to be tunnelled through in order to decay. This is true for some radioactive nuclei and for some electret materials able to carry electric charge for rather long periods.)

In general, a stable bound state is said to exist in a given potential of some dimension if stationary wavefunctions exist (normalized in the range of the potential). The energies of these wavefunctions are negative.

In relativistic quantum field theory, a stable bound state of n particles with masses m₁, ..., m_n shows up as a pole in the S-matrix with a center of mass energy which is less than m₁+...+m_n. An unstable bound state (see resonance) shows up as a pole with a complex center of mass energy.

Examples

A proton and an electron can move separately; the total center-of-mass energy is positive, and such a pair of particles can be described as an ionized atom. Once the electron starts to "orbit" the proton, the energy becomes negative, and a bound state - namely the hydrogen atom - is formed. Only the lowest energy bound state, the ground state is stable. The other excited states are unstable and will decay into bound states with less energy by emitting a photon.
A nucleus is a bound state of protons and neutrons (nucleons).
A positronium "atom" is an unstable bound state of an electron and a positron. It decays into photons.
The proton itself is a bound state of three quarks (two up and one down; one red, one green and one blue). However, unlike the case of the hydrogen atom, the individual quarks can never be isolated. See confinement.

In mathematical quantum physics

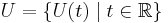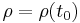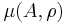Let $H$ be a complex separable Hilbert space, $U = \lbrace U(t) \mid t \in \mathbb{R} \rbrace$ be a one-parametric group of unitary operators on $H$ and $\rho = \rho(t_0)$ be a statistical operator on $H$ . Let $A$ be an observable on $H$ and let $\mu(A,\rho)$ be the induced probability distribution of $A$ with respect to $\rho$ on the Borel $\sigma$ -algebra on $\mathbb{R}$ . 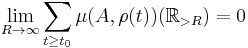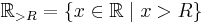Then the evolution of $\rho$ induced by $U$ is said to be bound with respect to $A$ if $\lim_{R \rightarrow \infty} \sum_{t \geq t_0} \mu(A,\rho(t))(\mathbb{R}_{> R}) = 0$ , where $\mathbb{R}_{>R} = \lbrace x \in \mathbb{R} \mid x > R \rbrace$ .

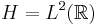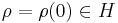Example: Let $H = L^2(\mathbb{R})$ and let $A$ be the position observable. Let $\rho = \rho(0) \in H$ have compact support and $[-1,1] \subseteq \mathrm{Supp}(\rho)$ .

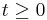If the state evolution of $\rho$ "moves this wave package constantly to the right", e.g. if $[t-1,t%2B1] \in \mathrm{Supp}(\rho(t))$ for all $t \geq 0$ , then $\rho$ is not a bound state with respect to the position.

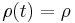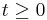If $\rho$ does not change in time, i.e. $\rho(t) = \rho$ for all $t \geq 0$ , then $\rho$ is a bound state with respect to position.

More generally: If the state evolution of $\rho$ "just moves $\rho$ inside a bounded domain", then $\rho$ is also a bound state with respect to position.

Covalent bonds	Sigma bond · Pi bond · Delta bond Double bond · Triple bond · Quadruple bond · Quintuple bond · Sextuple bond 3c–2e · 3c–4e · 4c–2e Agostic bond · Bent bond · Dipolar bond · Pi backbond Conjugation · Hyperconjugation · Aromaticity · Hapticity · Antibonding

Ionic bonds	Cation–pi bond · Salt bond

Metallic bonds	Metal aromaticity

Intermolecular
("weak")

Hydrogen bond	Dihydrogen bond · Dihydrogen complex · Low-barrier hydrogen bond · Symmetric hydrogen bond

Other noncovalent	van der Waals force · London dispersion force · Mechanical bond · Halogen bond · Aurophilicity · Intercalation · Stacking · Entropic force · Chemical polarity

Note: the weakest strong bonds are not necessarily stronger than the strongest weak bonds

Bound state

Examples

In mathematical quantum physics

See also